Μιλώντας για την φάση…

Η φάση ορίζεται για κάθε αρμονικά μεταβαλλόμενο εναλλασσόμενο μέγεθος και μας δείχνει πώς μεταβάλλεται το μέγεθος αυτό καθώς περνά ο χρόνος. Έτσι για κάθε μέγεθος που μεταβάλλεται σύμφωνα π.χ. με την εξίσωση:

V=V₀ημ(ωt+φ₀)

ορίζουμε φάση την ποσότητα:

φ=ωt+φ₀

όπου φ₀ η φάση του μεγέθους την χρονική στιγμή t₀=0.

Έτσι αν μιλάμε για μια απλή αρμονική ταλάντωση η εξίσωση της απομάκρυνσης είναι:

x=Α ημ(ωt+φ₀)

και η ποσότητα της οποίας παίρνουμε το ημίτονο, φ=ωt+φ₀ ονομάζεται φάση της απομάκρυνσης ή και απλά φάση της ταλάντωσης.

Ας δούμε κάποια παραδείγματα, για κατανοήσουμε τα παραπάνω.

Παράδειγμα 1^ο:

Δύο σώματα Β και Γ εκτελούν ταλαντώσεις του ίδιου πλάτους Α και της ίδιας περιόδου Τ. Τα σώματα ξεκινούν την ταλάντωσή τους για t₀=0, το πρώτο από την θέση ισορροπίας κινούμενο προς την θετική κατεύθυνση και το δεύτερο από την μέγιστη θετική απομάκρυνση.

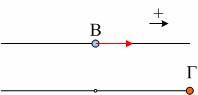
α) Ποια η αρχική φάση της ταλάντωσης κάθε σώματος;

β) Πόση είναι η φάση κάθε σώματος την χρονική στιγμή t₁=Τ/4;

Απάντηση:

α) Η απάντηση εύκολη, για το σώμα Β φ₀₁=0 και για το Γ φ₀₂= π/2 (rad).

Προσοχή: Πότε ξεκινούν τα σώματα; Όταν μηδενίζεται η φάση; Προφανώς ΟΧΙ. Αυτό συμβαίνει μόνο όταν δεν υπάρχει αρχική φάση φ₀.

β) την χρονική στιγμή t₁ τα σώματα έχουν φάσεις:

φ_Β=ωt+0= 2π/Τ·Τ/4=π/2 (rad)

φ_Γ=ωt+ π/2 = 2π/Τ·Τ/4+π/2= π (rad)

Παράδειγμα 2^ο:

Ένα σώμα για t₀=0 ξεκινά την ταλάντωσή του από τη θέση ισορροπίας και κινείται προς την αρνητική κατεύθυνση.

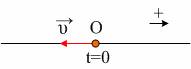
α) Η εξίσωση της απομάκρυνσής του είναι:

i) x= Α ημ(2πt+π) ή ii) x= - Αημωt

β) Ποια η φάση της απομάκρυνσης τη στιγμή t₁=1s;

Απάντηση:

α) Προφανώς οι δύο εξισώσεις είναι ισοδύναμες, πράγμα που σημαίνει ότι μπορούμε να χρησιμοποιήσουμε είτε την πρώτη είτε την δεύτερη, αν θέλουμε να μελετήσουμε την κίνηση του σώματος.

β) Για να βρούμε την φάση πρέπει ΥΠΟΧΡΕΩΤΙΚΑ να χρησιμοποιηθεί η πρώτη εξίσωση. Η φάση της ταλάντωσης δεν προκύπτει από την ii) εξίσωση. Έτσι:

φ=2πt+π = 3π (rad)

Μήπως το ότι έχει φάση 3π σημαίνει ότι έχει εκτελέσει 1,5 ταλαντώσεις; Σίγουρα το σώμα έχει κάνει μόνο ΜΙΑ ταλάντωση αφού Τ=t₁=1s, απλά τη στιγμή που ξεκινά την ταλάντωσή του είχε ήδη φάση ίση με π.

Παράδειγμα 3^ο:

Ένα σώμα εκτελεί ταυτόχρονα δύο α.α.τ. της ίδιας διεύθυνσης γύρω από την ίδια θέση ισορροπίας και με εξισώσεις:

x₁= 0,3 ημ2πt και x₂= - 0,5 ημ2πt (μονάδες στο S.Ι.)

α) Ποια η διαφορά φάσης των δύο ταλαντώσεων;

β) Ποια η φάση της ταλάντωσης του σώματος την χρονική στιγμή t₁=0,5;

Απάντηση:

α) Για να βρούμε την διαφορά φάσης θα πρέπει να ξαναγράψουμε την εξίσωση της απομάκρυνσης για την δεύτερη ταλάντωση:

x₂= - 0,5 ημ2πt = 0,5·ημ(2πt+π)

πράγμα που σημαίνει ότι η διαφορά φάσης μεταξύ των δύο ταλαντώσεων είναι π (rad).

β) Η απομάκρυνση του σώματος προκύπτει από την αρχή της επαλληλίας:

x=x₁+x₂= -0,2 ημ2πt = 0,2 ημ(2πt+π)

Και για t₁=0,5 έχουμε:

φ= 2πt+π = 2π (rad)

Παράδειγμα 4^ο:

Κατά μήκος ενός γραμμικού ελαστικού μέσου και από αριστερά προς τα δεξιά διαδίδονται δύο κυματομορφές, όπως στο σχήμα.

Τα σημεία Α και Β τη στιγμή που ελήφθη το στιγμιότυπο ξεκινούν την ταλάντωσή τους. Ποια είναι η φάση τους;

Απάντηση:

Το σημείο Α θα κινηθεί προς τα πάνω, θετική κατεύθυνση, ξεκινώντας από την θέση ισορροπίας του, συνεπώς φ_Α=0. Το σημείο Β βρίσκεται και αυτό στη θέση ισορροπίας του αλλά θα κινηθεί προς την αρνητική κατεύθυνση, άρα φ_Β=π (rad).

Παράδειγμα 5^ο:

Δίνεται ένα στιγμιότυπο ενός κύματος που διαδίδεται προς τα δεξιά και η εξίσωση του οποίου είναι y=0,2ημ2π(t-x+3/4). (Προφανώς Τ=1s και λ=1m). Τη στιγμή που ελήφθη το στιγμιότυπο η ταχύτητα του σημείου Ο στη θέση x=0 είναι μηδενική.

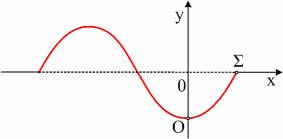
α) Ποια η φάση του σημείου Ο την στιγμή αυτή;

β) Σε ποια χρονική στιγμή αντιστοιχεί το παραπάνω στιγμιότυπο;

Απάντηση:

α) Το σημείο Σ έχει φάση π και το σημείο Ο έχει μεγαλύτερη φάση κατά π/2, συνεπώς έχει φάση 3π/2 rad

Το σημείο Σ που βρίσκεται στη θέση x=λ/4=0,25m έχει την στιγμή αυτή φάση φ=π. Οπότε:

2π(t-0,25+0,75) = π →

2(t+0,5) = 1→

2t + 1 = 1 →

t=0.

Συμπέρασμα:

Με βάση και την ανάρτηση: Περιστρεφόμενα διανύσματα και κύκλος αναφοράς Ταλάντωσης.) κάθε αρμονικά μεταβαλλόμενο μέγεθος μπορεί να θεωρηθεί ως η προβολή ενός περιστρεφόμενου διανύσματος. Η φάση είναι η γωνία του περιστρεφόμενου διανύσματος κάθε στιγμή με τον άξονα Οx.

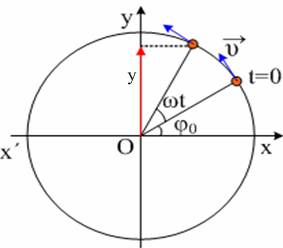
Δηλαδή αναφερόμενοι στο παραπάνω σχήμα όταν μια μικρή σφαίρα εκτελεί ομαλή κυκλική κίνηση, η θέση της κάθε στιγμή καθορίζεται από την γωνία που σχηματίζει το διάνυσμα θέσης με τον ημιάξονα Οx. Έτσι την τυχαία χρονική στιγμή t η γωνία αυτή είναι ωt+φ₀. Αν πάρουμε την προβολή του διανύσματος θέσης στον κατακόρυφο άξονα έχουμε y=Rημ(ωt+φ₀), παίρνουμε δηλαδή ένα μέγεθος που μεταβάλλεται αρμονικά με το χρόνο με φάση φ=ωt+φ₀, όπου φ₀ η αρχική γωνία του διανύσματος για t=0.

Αν αυτά γίνονται κατανοητά τότε μπορούμε να απαντήσουμε σε δύο ερωτήματα:

1) Είναι σωστή η πρόταση «Μηδενισμός φάσης σημαίνει έναρξη ταλαντωσης»;

Η πρόταση είναι λάθος. Προϋποθέτει φ₀=0. Να το πούμε με άλλα λόγια:

Στην ευθύγραμμη κίνηση που μελετάμε στην Α΄Λυκείου, μαθαίνουμε ότι άλλο θέση x και άλλο μετατόπιση Δx. Οι τιμές των μεγεθών συμπίπτουν μόνο αν για t=0 και x₀=0. Το ίδιο ακριβώς έχουμε και εδώ.

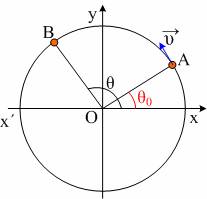
Αν έχουμε ένα σώμα που κάνει κυκλική κίνηση, άλλο η (γωνιακή) του θέση θ και άλλο η (γωνιακή) μετατόπισή του Δθ=θ-θ₀, όπου στο σχήμα είναι η γωνία ΑΟΒ.

Άλλο η φάση ενός μεγέθους φ=ωt+φ₀ και άλλο η μεταβολή της φάσης του Δφ=ωt.

2) Αναφερόμενοι σε ένα κύμα είναι λογικό να λέμε: «Η εξίσωση του κύματος πρέπει να έχει ένα μείον έξω».

Το ερώτημα θα το απαντήσουμε, αφού πρώτα επιλύσουμε ένα άλλο ερώτημα. Ένα σώμα βρίσκεται στο σημείο Α του παρακάτω σχήματος.

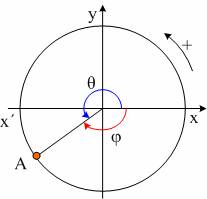
Η γωνία θ ή η γωνία φ δείχνει την γωνιακή του θέση; Εδώ πρακτικά είτε ξέρουμε την γωνία θ=210° είτε την γωνία φ=150°, η πληροφορία είναι ίδια. Χρειάζεται όμως παραπέρα επιχειρηματολογία γιατί στην γλώσσα των Μαθηματικών και της Φυσικής η γωνία θ=210° ενώ η φ= -150°; Όλοι ξέρουμε ότι έχει επικρατήσει να χρησιμοποιούμε την γωνία θ και όχι την γωνία φ.

Αν λοιπόν έχουμε μια ταλάντωση που το σώμα ξεκινά την ταλάντωσή του από την θέση ισορροπίας προς την αρνητική κατεύθυνση, ποια μπορεί να είναι η εξίσωσή του:

y= -Aημ(ωt) (1) ή y= A ημ(ωt+π) (2)

Υποστηρίζω ότι η σωστή εκδοχή είναι η (2). Γιατί; Ας δούμε τι σημαίνει η εκδοχή (1):

y= -Aημ(ωt) = Αημ(-ωt) ή

αναφερόμενοι στον παραπάνω κύκλο μελετά την κίνηση μετρώντας δεξιόστροφα τις γωνίες, ορίζει την θέση του σώματος με την γωνία φ και όχι με την θ. Μπορεί κάποιος να το κάνει; Ο καθένας μπορεί να ορίζει τα πράγματα με τον τρόπο που τον βολεύει, αλλά για να μπορούμε να συνενοούμαστε μεταξύ μας πρέπει να υπάρχει και ένας ορισμένος κώδικας επικοινωνίας….

dmargaris@sch.gr