Το Θ.Μ.Κ.Ε.
και η σύνθετη κίνηση

Με αφορμή μια συζήτηση στο βαθμολογικό……

Ερώτημα 1^ο:

Όταν μιλάμε για έργο, τι διαφορά έχει το έργο μιας δύναμης και το έργο μιας ροπής;

Στην πραγματικότητα έργο παράγει μια δύναμη, όταν μετατοπίζει το σημείο εφαρμογής της σε διεύθυνση που δεν είναι κάθετη στην μετατόπισή της. Δίνεται δε από τη γνωστή σχέση:

W=F·Δx·συνα

Όπου F το μέτρο της δύναμης, Δx το μέτρο της μετατόπισης και α η γωνία μεταξύ της δύναμης και της μετατόπισης.

Ο ορισμός αυτός ισχύει είτε στη μεταφορική είτε στην στροφική κίνηση. Είτε μελετάμε τη δράση μιας δύναμης σαν ΔΥΝΑΜΗΣ, είτε σαν ΡΟΠΗΣ.

Ας το δούμε αυτό μέσω παραδειγμάτων.

Παράδειγμα 1^ο:

Μια δύναμη F=10Ν ασκείται μέσω νήματος σε ένα σώμα και μετατοπίζει το σημείο εφαρμογής της κατά Δx=4m. Να βρεθεί το έργο της δύναμης, αν ασκείται:

i) στο σώμα Α που κινείται στο οριζόντιο επίπεδο.

ii) Εφαπτομενικά στον κύλινδρο, ο οποίος στρέφεται γύρω από σταθερό άξονα.

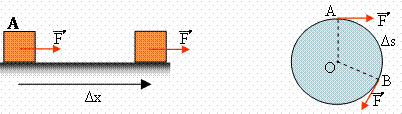
i) Η δύναμη στο πρώτο σχήμα μεταφέρει ενέργεια στο σώμα Α ίσο με το έργο της, που είναι W=F·Δx·συνα= 10Ν·4m= 40J.

ii) Και στο δεύτερο σχήμα η δύναμη μετατοπίζει το σημείο εφαρμογής της κατά Δx=Δs=4m, οπότε παράγει έργο W=F·Δx·συνα= 10Ν·4m= 40J.
Το μήκος όμως του τόξου ΑΒ Δs συνδέεται με την αντίστοιχη επίκεντρη γωνία Δθ με τη σχέση: Δs= Δθ·R, οπότε το έργο θα μπορούσε να γραφεί:

W=F·Δs·συν0°= F·Δs = F·Δθ·R= (F·R) ·Δθ= τ·Δθ

Μπορούμε δηλαδή να υπολογίσουμε το έργο της, αντιμετωπίζοντάς την σαν ροπή, οπότε:

W_τ =τ·Δθ

Παράδειγμα 2^ο:

Σε ένα λείο οριζόντιο επίπεδο ηρεμεί ένας κύλινδρος, μάζας m=4kg και ακτίνας R=0,5m, γύρω από τον οποίο τυλίγουμε ένα αβαρές νήμα. Σε μια στιγμή τραβάμε το άκρο Α του νήματος ασκώντας του σταθερή δύναμη F=10Ν. Ζητούνται:

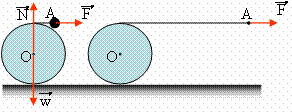
i) Η επιτάχυνση του κέντρου μάζας Ο του κυλίνδρου.

ii) Η γωνιακή επιτάχυνση του κυλίνδρου.

iii) Για χρονικό διάστημα Δt=4s να βρεθούν:

α) Η μετατόπιση και η ταχύτητα του άξονα του κυλίνδρου.

β) Η γωνιακή ταχύτητα και η γωνία περιστροφής του κυλίνδρου.

γ) Το ολικό έργο της δύναμης F.

δ) Το έργο της F, όσον αφορά τη μεταφορική κίνηση.

ε) Το έργο της ροπής της δύναμης.
Δίνεται για τον κύλινδρο Ι=1/2 m·R².
Να σχολιασθούν τα αποτελέσματα.

Απάντηση:

i) Για τη μεταφορική κίνηση του κυλίνδρου ισχύουν:

ΣF_y=0 και ΣF_x = ma_cm Þ

F=m·a_cm Þ a_cm=2,5m/s².

ii) Για την στροφική κίνηση του κυλίνδρου έχουμε (παίρνοντας σαν θετική φορά, τη φορά περιστροφής των δεικτών του ρολογιού):

Στ=Ι·α_γων Þ F·R= ½ m·R²·α_γων Þ

α_γων=2F/mR= 10rad/s².

iii) a) υ_cm = a·t = 2,5m/s²·4s= 10m/s και Δx=1/2 α·t² = ½ ·2,5·16m=20m.

β) ω=α_γων·t=40rad/s και Δθ= ½ α_γων·t²= ½ ·10·16 rad =80rad.

γ) Εξαιτίας της περιστροφής του κυλίνδρου ξετυλίχθηκε νήμα μήκους:

Δl=Δθ·R=40m, ενώ το άκρο Α, λόγω της μεταφορικής κίνησης μετατοπίσθηκε κατά Δx=20m. Άρα η μετατόπιση του σημείου εφαρμογής της δύναμης είναι Δx_ολ=60m. Κατά συνέπεια:

W_F=F·Δx·συν0°=10·60·1J=600J.

δ) Αν πάρουμε μόνο τη μεταφορική κίνηση: W₁=F·Δx=200J.

ε) Για το έργο της ροπής: W_τ=W₂= τ·Δθ=F·R·Δθ=400J.

Πραγματικά ο κύλινδρος λόγω μεταφορικής κίνησης έχει αποκτήσει κινητική ενέργεια:

Κ_μετ = ½ mυ_cm²= ½ 4·100J =200J, όσο και το W₁,

ενώ εξαιτίας της στροφικής του κίνησης:

Κ_στρ = ½ Ιω² = ½ ½ mR²ω²= ¼ 4·0,25·40²J = 400J,

όσο είναι και το αντίστοιχο έργο της ροπής, εξαιτίας της οποίας και περιεστράφη ο κύλινδρος.

Με βάση το προηγούμενο παράδειγμα, θα μπορούσαμε να διατυπώσουμε το συμπέρασμα ότι:

«Αν ένα σώμα κάνει σύνθετη κίνηση και πάνω του ασκείται μία ή περισσότερες δυνάμεις, τότε το έργο τους (σαν δυνάμεις, οπότε επηρεάζουν τη μεταφορική κίνηση) θα συνδέεται με τη μεταβολή της μεταφορικής κινητικής ενέργειας του σώματος, ενώ το έργο τους (ως ροπές, οπότε επηρεάζουν την περιστροφική κινητική ενέργεια του σώματος) θα ισούται με τη μεταβολή της περιστροφικής κινητικής ενέργειας του στερεού.»

Οπότε ανακύπτει το:

Ερώτημα 2^ο:

Σε μια σύνθετη κίνηση, μπορούμε να πάρουμε το θεώρημα έργου – ενέργειας (Θ.Μ.Κ.Ε) μόνο για τη μεταφορική ή μόνο για την στροφική του κίνηση ή θα πρέπει να εφαρμόζεται ΜΟΝΟ για τη συνολική κίνηση;

Αν και με βάση το προηγούμενο παράδειγμα, η απάντηση είναι προφανής, ας το εξετάσουμε γενικά με βάση τα Μαθηματικά.

Αξίζει εδώ να τονισθεί ότι το Θ.Μ.Κ.Ε. δεν είναι κάποιος γενικός νόμος της φύσης (όπως η αρχή διατήρησης της ενέργειας) αλλά αυτό που λέει το όνομά του. Ένα Θεώρημα.

Ας το αποδείξουμε λοιπόν.

Ένα στερεό, ο κύλινδρος στο παραπάνω παράδειγμα, που εκτελεί σύνθετη κίνηση, έχοντας υ_cm=υ₀ και γωνιακή ταχύτητα ω₀, δέχεται σε μια στιγμή, μια σταθερή δύναμη F στην κατεύθυνση της ταχύτητας υ_cm, η οποία έχει και ροπή ως προς τον άξονα περιστροφής.

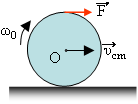
Για τη μεταφορική του κίνηση θα ισχύουν:

F=m·a_cm Þ α_cm = F/m οπότε υ_cm = υ = υ₀+ α_cm t (1) και x=υ₀t+ ½ α_cmt² (2)

Λύνοντας την (1) ως προς t παίρνουμε t=(υ-υ₀)/αcm και με αντικατάσταση στην (2) παίρνουμε:

χ= υ₀·(υ-υ₀)/αcm+ ½ α_cm·[(υ-υ₀)/αcm]² = (υ² – υ₀²)/2αcm

Παίρνουμε τώρα το έργο της δύναμης για μετατόπιση κατά x και έχουμε:

W_F= F·x= m·α_cm ·(υ² – υ₀²)/2αcm = ½ mυ²- ½ mυ₀² (1^α)

Ή αλλιώς W_F= Κ_τελ-Κ_αρχ.

Βλέπουμε ότι ΜΟΝΟ για τη μεταφορική κίνηση του σώματος

το θεώρημα ΙΣΧΥΕΙ.

Ας έλθουμε τώρα στην στροφική κίνηση:

Στ=Ι·α_γων, οπότε ω=ω₀ + α_γων·t (3) και Δθ=ω₀·t + ½ α_γων·t² (4)

Λύνοντας την (3) ως προς t παίρνουμε t=(ω-ω₀)/α_γων και με αντικατάσταση στην (4) παίρνουμε:

Δθ= ω₀·(ω-ω₀)/α_γων + ½ α_γων·[(ω-ω₀)/α_γων]² =(ω²-ω₀²)/2α_γων.

Οπότε παίρνοντας το έργο της ασκούμενης ροπής έχουμε:

W_τ = προς·Δθ = Ι·α_γων · (ω²-ω₀²)/2α_γων = ½ Ι·ω² – ½ Ιω₀². (2^α)

Ή αλλιώς Wτ= Κπερ_τελ – Κπερ_αρχ.

Αποδείξαμε δηλαδή ότι το Θ.Μ.Κ.Ε. ισχύει αν εφαρμοστεί ΜΟΝΟ για την στροφική κίνηση του στερεού.

Βέβαια αν προσθέσουμε κατά μέλη τις εξισώσεις (1^α) και (2^α) θα έχουμε:

W_F+ W_τ = (½ mυ² + ½ Ιω²) – ( ½ mυ₀² + ½ Ιω₀²)

Ή διαφορετικά: W_Fολ = Κ_ολτελ – Κ_ολτελ.

Εξίσωση που μας λέει ότι το θεώρημα ισχύει και για την σύνθετη κίνηση.

Μια εφαρμογή των παραπάνω:

Εφαρμογή 1^η:

Σε οριζόντιο επίπεδο ηρεμεί ένας κύλινδρος μάζας 20kg και ακτίνας R=0,5m. Σε μια στιγμή δέχεται μια σταθερή οριζόντια δύναμη μέτρου F=30Ν, όπως στο σχήμα. Αν δίνεται ότι ο κύλινδρος αρχίζει να κυλίεται χωρίς ολίσθηση ενώ η ροπή αδράνειας του κυλίνδρου ως προς τον άξονά του Ι=1/2 m·R², να βρεθούν για χρονικό διάστημα t=4s:

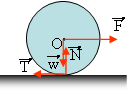
α) Η επιτάχυνση του άξονα του κυλίνδρου, η γωνιακή του επιτάχυνση και το μέτρο της ασκούμενης τριβής.

β) Η ταχύτητα και η μετατόπιση του άξονα του κυλίνδρου.

γ) Η γωνιακή ταχύτητα και η γωνία περιστροφής του κυλίνδρου.

δ) Το έργο της δύναμης F και το έργο της τριβής.

ε) Πώς συνδέεται η μεταφορική και η περιστροφική κινητική ενέργεια του κυλίνδρου με τα έργα των δυνάμεων;

Λύση:

α) Για τη μεταφορική κίνηση έχουμε:

ΣF=m·α_cm ή F-Τ = m·a_cm (1)

ενώ για τη στροφική κίνηση:

Στ= Ι·α_γων ή T·R = ½ mR²·α_γων ή Τ= ½ mR·α_γων. (2)

Επειδή όμως ο κύλινδρος κυλίεται χωρίς ολίσθηση ισχύει α_cm =α_γων·R και με πρόσθεση κατά μέλη των (1) και (2) λαμβάνουμε:

F= ½ mRα_γων + mα_cm ή F= 3/2 mα_cm ή α_cm = 2F/3m και με αντικατάσταση:

α_cm =2·30/3·20m/s² =1m/s².

Οπότε και α_γων = α_cm/ R= 2rad/s².

Και από τη σχέση (1) έχουμε Τ=F-m·α_cm=(30-20·1)Ν=10Ν

β) Η μεταφορική κίνηση του σώματος είναι ευθύγραμμη ομαλά επιταχυνόμενη άρα υ=α_cm·t =1m/s²·4s =4m/s και x= ½ a_cm·t²= ½ 1m/s²·16s² =8m.

γ) Η στροφική κίνηση του κυλίνδρου είναι ομαλά επιταχυνόμενη, οπότε:

ω=α_γων·t = 2rad/s²·4s=8rad/s και θ= ½ α_γων·t²= ½ ·2·16 rad=16rad.

δ) Για τα έργα των δυνάμεων έχουμε:

W_F= F·x·συν0°=30Ν·8m=240J.

W_Τ =Τ·Δx·συν180°=10Ν·0=0 J

Αφού η τριβή είναι στατική, δεν μετατοπίζεται το σημείο εφαρμογής της ( η ταχύτητα του σημείου εφαρμογής της είναι μηδενική), κατά συνέπεια δεν παράγει έργο.

Ε) Ο κύλινδρος έχει μεταφορική κινητική ενέργεια:

Κ₁= ½ mυ² = ½ 20·16 J=160J

Και περιστροφική κινητική ενέργεια:

Κ₂ = ½ Ι ω² = ½ ½ mR²ω²= ¼ 20·0,25·64 J= 80J

Ας παρατηρήσουμε ότι η ολική κινητική ενέργεια που απέκτησε ο κύλινδρος είναι Κ₁+Κ₂= 240J = W_F, αφού μόνο η δύναμη F μεταφέρει ενέργεια στο σώμα.

Ερώτημα 3^ο:

Δηλαδή στην παραπάνω εφαρμογή μπορούσαμε να χρησιμοποιήσουμε το θεώρημα έργου – ενέργειας μόνο για τη μεταφορική ή μόνο για την στροφική κίνηση; Και αν ναι, γιατί να το κάνουμε; Υπάρχει λόγος;

Η απάντηση μπορεί να προκύψει, αν αναρωτηθούμε γενικά ποιος ο λόγος που χρησιμοποιούμε το μέγεθος έργο. Τι εκφράζει το μέγεθος αυτό, τι πληροφορίες μας δίνει;

Οι γνωστές ιδέες:

• Το έργο μετράει την ενέργεια που μεταφέρεται από ένα σώμα Α σε ένα άλλο Β. Μετράει λέμε τη μεταφορά ενέργειας.
• Το έργο μετράει την ενέργεια που μετατρέπεται από μια μορφή σε μια άλλη. Μετράει δηλαδή τη μετατροπή ενέργειας.

Στην παραπάνω εφαρμογή πώς δικαιολογούνται τα παραπάνω;

Το έργο μιας δύναμης F μετράει την ενέργεια που μεταφέρεται από αυτόν που ασκεί τη δύναμη στον κύλινδρο. Κανένα πρόβλημα. Το έργο της τριβής είναι μηδέν, άρα ούτε δίνει ούτε παίρνει ενέργεια.

Ναι, αλλά πώς γίνεται το μοίρασμα μεταξύ μεταφορικής και κινητικής ενέργειας; Υπάρχει κάποιο έργο για να μετρήσουμε αυτήν την μετατροπή; Η τριβή παίζει κάποιο ρόλο;

Η απάντηση είναι πώς ΝΑΙ. Η τριβή είναι αυτή που προκαλεί την περιστροφή του κυλίνδρου. Αρκεί να σκεφτούμε ότι, αν το επίπεδο ήταν λείο, ο κύλινδρος δεν θα στρεφόταν και αν μεταφερόταν ενέργεια από τη δύναμη F ίση με 240J, αυτή θα εμφανιζόταν μόνο με τη μορφή της μεταφορικής κινητικής ενέργειας.

Και πώς πάνε τώρα λοιπόν τα πράγματα;

• Ας εφαρμόσουμε το Θ.Μ.Κ.Ε. μόνο για τη μεταφορική κίνηση του κυλίνδρου και για μετατόπιση κατά x=8m ας υπολογίσουμε την ταχύτητα που αποκτά ο κύλινδρος.

Κ_τελ-Κ_αρχ = W_F+ W_Τ+W_w+W_Ν. ενώ W_w=W_Ν=0

Αφού οι δυνάμεις είναι κάθετες στη μετατόπιση και Κ_αρχ = 0, οπότε:

½ mυ² = F·x·συν0° + Τ·x·συν180° ή ½ mυ² = 30·8J-10·8J ή

½ mυ² =240 J -80 J από όπου υ= 4m/s.

Παρατηρούμε ότι μπορούμε να χρησιμοποιήσουμε το θεώρημα έργου – ενέργειας για να υπολογίσουμε την τελική ταχύτητα του κυλίνδρου. Στην παραπάνω εξίσωση μπαίνει έργο για την ΣΤΑΤΙΚΗ τριβή και υπολογίζεται ίσο με – 80J. Ποια η φυσική του σημασία;

Όσον αφορά τη μεταφορική κίνηση του σώματος η στατική τριβή αφαιρεί ενέργεια 80J από τον κύλινδρο.

Και τι την κάνει;;;

• Εφαρμόζουμε το Θ.Μ.Κ.Ε. μόνο για τη στροφική κίνηση και για περιστροφή κατά γωνία θ=16rad και έχουμε:

Κ_τελ- Κ_αρχ = Wτ ή ½ Ιω² = τ·θ ή ½ Ι·ω² = ΤR·θ ή

½ Ι·ω² = 10· 0,5·16J ή ½ Ι·ω² =80J

από όπου παίρνουμε: ω= 16rad/s.

Βλέπουμε δηλαδή ότι όση ενέργεια αφαιρεί από τη μεταφορική κίνηση η τριβή (σαν δύναμη) την μετατρέπει σε κινητική περιστροφική ενέργεια, μέσω του έργου της ροπής της.

Και αν η τριβή δεν είναι στατική;

Εφαρμογή 2^η:

Σε οριζόντιο επίπεδο ηρεμεί ένας κύλινδρος μάζας 20kg και ακτίνας R=0,5m. Σε μια στιγμή δέχεται σταθερή οριζόντια δύναμη μέτρου F=120Ν, όπως φαίνεται στο σχήμα. Οι συντελεστές τριβής μεταξύ κυλίνδρου και επιπέδου είναι μ_s=μ=0,15. Αν δίνεται η ροπή αδράνειας του κυλίνδρου ως προς τον άξονά του Ι= ½ m·R² και g=10m/s², να βρεθούν για χρονικό διάστημα t=4s:

α) Η ταχύτητα του άξονα και η γωνιακή ταχύτητα του κυλίνδρου.

β) Η μετατόπιση του άξονα του κυλίνδρου και η γωνία περιστροφής του.

γ) Τα έργα της δύναμης F και της τριβής (ως δύναμης για τη μεταφορική κίνηση)

δ) Το έργο της ασκούμενης ροπής.

ε) Την ενέργεια που μετατρέπεται σε θερμική.

Λύση:

a) Το βασικό ερώτημα είναι αν ο κύλινδρος ολισθαίνει ή όχι.

Υποθέτουμε λοιπόν ότι ο κύλινδρος κυλίεται χωρίς να ολισθαίνει, οπότε θα ισχύει και η γνωστή μας σχέση υ_cm = ωR και έχουμε:

ΣF_y= 0 ή Ν=mg και ΣF_x =m·α_cm ή F-Τ = m·α_cm (1)

Στ=Ι·α_γων ή Τ·R = ½ m·R²·α_γων ή Τ= ½ mRα_γων (2)

Και με πρόσθεση κατά μέλη των (1) και (2) βρίσκουμε:

F= mα_cm + mRα_γων ή F= 3/2 mα_cm

από όπου α_cm= 2·120/3·20m/s² = 4m/s².

Βρίσκουμε τώρα το μέτρο της τριβής από την (2)

Τ= ½ mα_cm= ½ 20·4Ν= 40Ν

και την συγκρίνουμε με την μέγιστη δυνατή τιμή που μπορεί να πάρει, δηλαδή με την οριακή τιμή της τριβής, που είναι:

Τ_ορ=μ_sΝ= μ·Ν=μmg= 0,15·20·10Ν=30Ν.

Βλέπουμε ότι Τ>Τ_ορ άρα η υπόθεσή μας ότι ο κύλινδρος κυλίεται χωρίς να ολισθαίνει δεν ευσταθεί. Ο κύλινδρος ολισθαίνει και η ασκούμενη τριβή είναι ολίσθησης με μέτρο Τ=30Ν.

Από την εξίσωση (1) παίρνουμε α_cm=(F-Τ)/m =(120-30)/20 m/s² =4,5m/s², ενώ από τη σχέση (2) έχουμε α_γων= 2Τ/mR =2·30/20·0,5 rad/s²=6rad/s².

Έτσι για τις ταχύτητες έχουμε:

υ_cm= α_cm·t= 4,5m/s²·4s =18m/s και

ω= α_γων·t=6rad/s²·4s=24rad/s.

β) Η μετατόπιση του άξονα του κυλίνδρου είναι x= ½ α_cm·t² = ½ 4,5 · 16m= 36m, ενώ η γωνία περιστροφής: θ= ½ α_γων·t² = ½ 6·16rad=48 rad.

γ) Τα έργα των δυνάμεων είναι:

W_F= F·x·συνθ =120Ν·36m·1=4320 J και

W_Τ =Τ·x·συν180°=30Ν·36m·(-1)= - 1080 J

Να σημειωθεί ότι το παραπάνω έργο είναι της τριβής μόνο για τη μεταφορική κίνηση.

δ) Το έργο της ροπής της τριβής είναι:

W_τ= τ·θ =Τ·R·θ =30Ν·0,5m·48 = 720 J

ε) Από τα παραπάνω βλέπουμε ότι μέσω της τριβής αφαιρείται ενέργεια 1080 J ενώ μόνο 720J μετατρέπονται σε περιστροφική κινητική ενέργεια. Τα υπόλοιπα; Η υπόλοιπη είναι η ενέργεια που μετατρέπεται σε θερμική,

δηλαδή Q=|-1080J| –| 720 J| =360 J.

(Για περισσότερα πάνω στο έργο της τριβής, δείτε

«μερικοί μύθοι για την ΤΡΙΒΗ»)

Γιατί είναι τόση η θερμική ενέργεια;

Βρήκαμε ότι ο κύλινδρος περιεστράφη κατά θ= 48rad, γωνία στην οποία αντιστοιχεί τόξο s=θ·R= 48·0,5m =24m και αφού η οριζόντια μετατόπιση του κυλίνδρου είναι x=36m, ο κύλινδρος γλίστρησε κατά:

X₁=x-s =36m-24m =12m

Οπότε η μηχανική ενέργεια που μετατρέπεται σε θερμική είναι:

Q = |Τ·Χ₁|= 30Ν·12m=360 J.

Μπορείτε να κατεβάσετε το αρχείο σε pdf.

dmargaris@sch.gr